A long-term travel delay measurement study based on multi-modal human mobility data

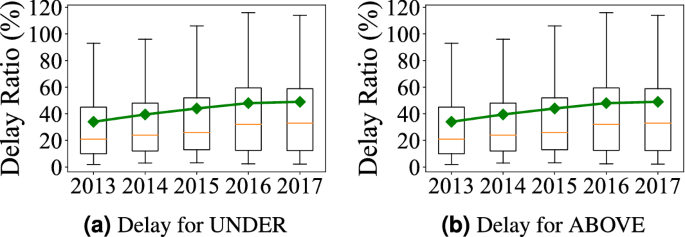
Travel delay from 2013 to 2017.

Individual evolving patterns

Quantitative results

The box distribution of all trips’ delay is used where the top and bottom of each box are the 25th and 75th percentiles; the middle red lines are the median values; the top and bottom of each black dash lines indicate the maximal and minimal values. Figure 1a, b show the delay ratio distributions in underground systems (i.e., Subway) and aboveground systems (i.e., combining taxi, bus, and PV) from 2013 to 2017 where we made three observations as follows.

Observation 1 in Fig. 1: For both underground and aboveground, both travel delay and variance increase each year We analyze Shenzhen census data, which shows the high-level statistics about the mobility demand/supply and population change. We process the census data from 2011 to 2016 and normalize all absolute values to relative differences from the values of the first year, i.e., 2011, to show evolving patterns of travel demand and supply. Increasing Overall Demand Figure 2a gives Shenzhen Travel Demand by the number of passengers for subway; the number of personal vehicles (i.e., cars); Shenzhen citywide permanent population. We found that (1) the permanent population increases from 10.47 million to 11.91 million (13.8%); (2) the number of cars increases from 1.98 million to 3.23 million (63.3%); (3) the annual use of subway passengers increases from 0.4 billion to 1.2 billion (177.1%). Decreasing per-capita Supply Figure 2b shows Shenzhen Travel Supply by the length of roads per capita; the length of subway systems (in terms of km) per capita. We found that even increasing in the absolute length, both travel supply for both aboveground system and underground system decrease per capita due to increasing population and travel demand as shown in Fig. 2a. A combination of the increasing overall demand and decreasing per-capita supply leads to our observation.

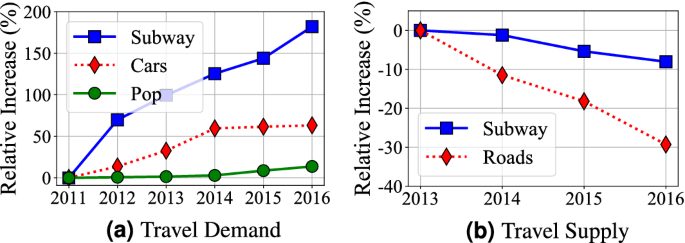
Travel demand and supply evolving.

Observation 2 in Fig. 1: The aboveground systems have a slow-down delay increase compared to the underground system To explore the reason, we refer to Fig. 2a where we found that the increase of cars slows down from 2015. We further explore to find out that to control the increase of personal cars and alleviate the traffic congestion, from 2015, the Shenzhen government implemented a license lottery policy on personal cars¹⁸. In the license-plate lottery policy, residents submit applications for vehicle license plates each year but only certain number of applications will be approved. Therefore, the increasing speeds of personal cars became much slower since 2015. Since personal cars account for the major aboveground system delay, its slower car increase leads to our observation “the aboveground system has a slow-down delay increase”.

Observation 3 in Fig. 1: The underground system has lower increased delay overall compared to the aboveground one To explore the reason, we refer to Fig. 2b where even both the underground system and aboveground system have decreasing per-capita supply, the underground system supply decreasing rate is much lower than that of aboveground system, due to the fast building of Shenzhen Subway System (i.e., increasing from 178.341 to 285.528 km in these 5 years). As a result, even though (1) the underground system has a strongly increasing demand (177.1%) and (2) the aboveground system has an almost-stopped increasing demand (due to license lottery policy, Shenzhen only have 2.2% more registered cars from 2014 to 2016), the underground system’s overall increase delay is still lower than the aboveground system. It might suggest that increasing supply is better than controlling demand.

Statistic significance of observation 1, 2, and 3

To validate the statistical significance of data for the above three observations, we put the average delay of all origin-destination pairs in a year in a vector, and then report the test results of the statistical difference between the delays of two consecutive years. Table 1 shows the results of two statistical tests, for each cell, the shadowed background means it is statistically significant in Mann–Whitney U test¹⁹ and the value in the cell is the \({\mathscr{A}}\) measure in Vargha–Delaney²⁰. We found that all travel delay differences between consecutive years from 2013 to 2017 are statistically significant by both two tests. The \({{\mathscr{A}}}\) measure confirms the travel delay increases with time in the city, i.e., \({{\mathscr{A}}} > 0.5\). We observed a relatively smaller number in 16–17 when comparing ABOVE with UNDER, the potential reasons are increasing demand of UNDER, while the travel delay for ABOVE has a relatively small number due to car policy, a relatively larger baseline of delay for ABOVE in 2016, and upgrade of ABOVE road networks.

Cross-modal evolving patterns

For a rigorous cross-modal investigation, we study the impact of the aboveground system and the underground system infrastructure upgrades (e.g., new roads or new subway lines) on travel delay in two categories of areas: (1) Test areas (Test): city areas covered by the infrastructure upgrades based on our spatial partition. (2) Control areas (Control): city areas not covered. We calculate population distribution, delay ratio, and ratio increase speed in the test areas before infrastructure upgrades, and then we select control areas with similar features.

A travel delay ratio is defined with five attributes in Eq. 3 in both underground and aboveground systems. With the same \(\theta \) and temporal partition, we apply a spatial alignment on the two systems to study the cross-modal impact under the same spatio-temporal dimension. Specifically, we map both the underground system and the aboveground system partitions into 497 administrative regions released by government based on the their overlap areas.

Impact of aboveground system infrastructure upgrades

We collect data about the aboveground system infrastructure upgrades (e.g., road open time) by analyzing OpenStreetMap data²¹ on social media. We found 653 km of roads were constructed and taken into services during 2013 and 2017, i.e., 6015 km of total road length at the beginning of 2013, and 6668 km of total road length at the end of 2017.

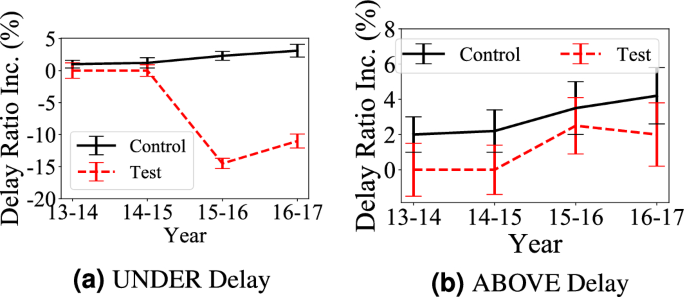
Delay increase in underground or aboveground areas covered by aboveground upgrades (test areas) and similar area not covered by aboveground upgrades (control areas).

Citywide Trend To compare the impact of aboveground system infrastructure upgrades (i.e., new roads) on travel delay in both aboveground and underground systems, Fig. 3 presents mean and standard deviation of delay ratio increase, i.e., the absolute delay ratio difference, during 5 years in the two groups.

Observation 4 in Fig. 3a: The aboveground system infrastructure upgrades increase the aboveground travel delay When we compare test areas with control areas. Based on the locations of the aboveground system upgrade, we found that they mostly happen in suburban areas since the downtown areas are well-developed and out of space for new roads. As a result, these the aboveground system upgrades enable residents in suburban areas to take new roads to transfer to subways to go to downtown, which leads to increased the underground system travel delay in test areas. Based on results in Fig. 3b, we found some expected results: the aboveground system upgrades decrease the aboveground travel delay. This is an obvious observation since new roads decrease both travel distance in connected areas and travel volumes on existing roads.

Statistical Significance of Observation 4 We conduct U-test and A-test on different origin-destination pairs and the results are reported in Table 2. The shadowed cells indicate the travel delay differences are statistically significant with U-test. The number in the table is \({{\mathscr{A}}}\) measures of A-test. The results show the aboveground system upgrades have (1) a positive impact on the aboveground system delay, e.g., the aboveground system delay in Test Area decreases from 0.71 to 0.33 while the aboveground system delay in Control Area increases from 0.69 to 0.78; (2) a negative impact on the underground system delay, e.g., the underground system delay in Test Area significantly increases from 0.61 to 0.79 while the underground system delay in Control Area slightly increases from 0.65 to 0.68.

A Case Study of Aboveground System Upgrades We take a major highway (Guangshen Yanjiang Expressway) connecting Shenzhen airport, residential areas, and CBD areas for measurement, which was open at the end of 2013.

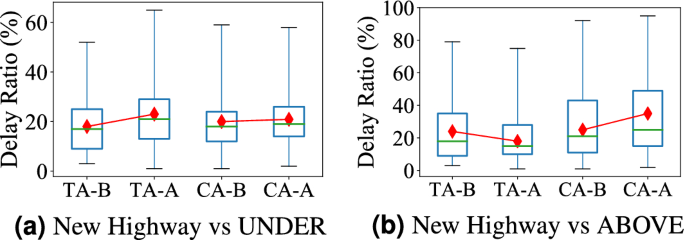
Impact of new highway; (a) new highway increases underground delay in test areas after open (TA-A); (b) new highway decreases aboveground delay in test areas after open.

Figure 4a shows the delay comparison for the underground system between the Test areas (impacted by the new highway) and Control areas (not impacted by the new highway) one month before and after this new highway was put into services. Similarly, Fig. 4b shows the travel delay comparison for the aboveground system.

(1) As shown in Fig. 4a, this highway significantly increases the underground system delay in the Test Area (from 18 to 24%) while the underground system delay in the Control Area only slightly increases (from 20 to 21%). This is because this highway (far-reaching to remote areas) brings more passengers for two major subway stations at one end of the highway, leading to increase the delay in these stations. This result is consistent with our Observation 4 on citywide trend. (2) As shown in Fig. 4b, this highway decreases the aboveground system delay in the Test Area (from 22 to 18%) while the aboveground system delay in the Control Area significantly increase (from 23 to 36%). The new highway directly decreases the travel time in the aboveground system by decreasing the travel distance and improving the traffic conditions. This result is consistent with our Observation 5 on citywide trend.

Impact of the underground infrastructure upgrades

In Shenzhen, three subway lines and 68 stations were added to the subway system in 2016 and 2017.

Citywide Trend To compare the impact of the underground system infrastructure upgrades (the underground system upgrade hereafter, i.e., new stations) on travel delay in both systems, Fig. 5 shows the delay ratio increase, i.e., the absolute delay ratio difference, during 5 years in the test areas (impacted by the underground system upgrades) and control areas (not impacted by the underground system upgrades but with similar demographic and geographic features). Since the aboveground system upgrade only happens in 2016 and 2017, the delay increases in 2014 and 2015 in test areas are 0.

Delay increase in underground or aboveground areas with underground upgrades (test areas) and similar areas have no aboveground upgrades (control areas).

Observation 5 In Fig. 5a, an expected observation is that the underground system upgrades decrease travel delay in the underground system by 14% (absolute difference) due to increased underground supply. Figure 5b: The aboveground system infrastructure upgrades slows down the aboveground system travel delay increase From 3.5 to 2%, even though the travel delay still increases in test areas. We found most underground system upgrades happen in downtown areas with high travel demand. The underground system upgrades decrease travel demand in the existing aboveground system and lead to lower traffic increase in the aboveground system. This is also supported by the previous literature outcomes such as a mismatch between demand increase and travel infrastructure upgrades^22,23,24.

Statistical Significance of Observation 5 We further measure the difference by the two tests, and their results are reported in Table 3. The shadowed cells show the travel delays are statistically significant by U-test. The values of \({{\mathscr{A}}}\) measure show underground upgrades have (i) a positive impact on the aboveground travel delay, e.g., the \({{\mathscr{A}}}\) measure of aboveground travel delay in Test Areas slows down from 0.68 to 0.53 while the \({\mathscr{A}}\) measure of aboveground travel delay in Control Areas increases from 0.66 to 0.71; (2) a positive impact on the underground travel delay, e.g., the \({\mathscr{A}}\) measure of underground travel delay in Test Areas decreases from 0.61 to 0.28 while the \({{\mathscr{A}}}\) measure of underground travel delay in Control Areas increases from 0.61 to 0.63.

A Case Study of Underground System Upgrades We investigate the impact of subway line NO.7 opened in 2016, which has a length of 30.1 km and includes 27 stations. For the underground system, we study how the new stations influence travel delays of overloaded stations. Figure 6a shows the travel delay comparison for the underground system. Figure 6b shows the travel delay comparison for the aboveground system between Test areas (impacted by the new subway line) and Control areas (not impacted by the new subway line) one month before and after this new subway line was taken into services.

Impact of new stations; (a) it decreases the travel delay in the underground system; (b) it decreases the travel delay in the aboveground system.

(1) As shown in Fig. 6a, this new subway line decreases underground delay in Test areas significantly (from 36 to 18%) while the underground system delay in control areas increases slightly (from 19 to 20.6%). This is because the subway line passes through central business areas and is connected with 6 existing subway lines. It reduces passengers in existing stations, reduce the travel distance and transfer time. The result is consistent with our Observation 6 on citywide trend. (2) As shown in Fig. 6b, the new subway line slows down the travel delay increase in the Test areas (0.9% delay ratio increase compared with 3.2% delay ratio increase in Control areas). This is because more passengers choose the subway and it slows down the passenger demand increase in the aboveground systems. The result is consistent with our Observation 5 on the citywide trend.

Contextual factors

We measure the impact of five contextual factors on delay ratio of the underground system (i.e., subway) and the aboveground system (i.e., car, bus, taxi), i.e., population, temporal, spatial, weather, social event, and West Texas Intermediate (WTI) crude oil price.

Correlation between travel delay and population: (a) the underground system’s delay is low in populous regions; (b) the aboveground system’s delay is high in populous regions.

(1) Population

Population distribution is one of the most important and unexpected factors for travel delay. For the underground system, we map the population to stations based on the walking distance in a non-overlapping partition where the average distance between adjacent stations in the subway system is 1.16 km, so we set the walking distance as half of the average distance, i.e., 0.58 km, which leads to the walking area of \(1.05\,{\text {km}}^2\)²⁵. 78.4% of regions in the coverage areas of the subway system have more than 10,000 population because the subway system covers the most downtown areas. For the aboveground system, we map the population to grids and investigate the relationship between population and delay at the grid level. The grid size we investigate is \(1.37\,{\text {km}}^2\). 77.1% of grids have less than 10,000 population. In Fig. 7a, b based on different populations on the X-axis, we show both the ratio of regions among all regions (Left Y-Axis) and average the underground system delay in these regions (Right Y-axis). Observation 6 the underground travel delay decreases with the higher population; whereas the aboveground system travel delay increases with the higher population. This is mainly because of the different flexibility of underground system and the aboveground system supply, even with the same increasing demand. For the underground system in high population regions, both higher train frequency and denser subway system deployment are used for higher the underground system supply per passenger in populous areas. However, for the aboveground system, a higher the aboveground system supply is not possible in populous regions since the space for the aboveground system infrastructure upgrades (e.g., new road) is limited in the populous regions. Another minor observation is that the degree of the aboveground system travel delay increasing is smaller in grids with more than 20,000 population. This may be because the dense regions (e.g., downtown CBD) have better road structures.

Delay distribution during one day; (a) underground travel delay is dominated by train frequency; (b) aboveground travel delay is dominated by spatial entropy.

(2) Temporal Fig. 8 presents travel delay during one day in UNDER and ABOVE system. Observation 7 the underground system travel delay decreases during peak hours (7 am to 9 am and 4 pm to 8 pm); whereas the aboveground system travel delay increase during peak hours. For example, there are a lower travel delay in the underground system (around 13% on average) and a higher travel delay in the aboveground system (around 50% on average). For the underground system, the subway system sends trains more frequently in peak hours as shown in Fig. 8a, i.e., the 5-min time interval in the peak hours and the 8.5-min time interval in the off-peak hours²⁶. Sending trains more frequently reduces the waiting time significantly while increases the operational cost. For instance, a subway line with 1 h of total travel time requires at least 7 subway trains (1 h/8.5 min) to maintain services in off-peak hours but 12 trains in peak hours (1 h/5 min). It increases the operational cost by 71% (from 7 trains to 12 trains). For the aboveground system, we found a lower entropy (lower randomness) in taxis and personal vehicles as shown in Fig. 9a during the peak hours. In other words, taxis and personal cars concentrate on commuting between certain areas, e.g., work areas and home areas, during peak hours, which leads to increased the aboveground system delay. Figure 9b shows the weekly patterns where we found a higher travel delay on weekdays than weekends in the aboveground system by 25% during peak hours, while the difference is negligible in the underground system.

(3) Spatial In both systems, travel delay increase by years in downtown areas because of higher travel demand in the downtown areas (where most regions with Top k delay ratios reside) with a limited improvement of infrastructures. In contrast, the general trend of suburban areas in both systems is decreasing by years. This is because the better infrastructures are constructed in suburban areas, e.g., roads and subway stations, along with Shenzhen urbanization. Comparing the underground and aboveground systems, we found the impact of infrastructure upgrades on the underground system is larger than the aboveground system because a new subway line can cover large areas and can even function as transfer lines to decrease the travel time between the existing two stations.

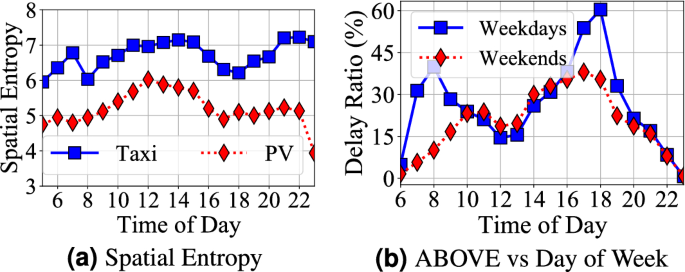
(a) A lower spatial entropy means lower randomness on spatial dimension and cars moves to certain areas; (b) lower peak hour and shifts on weekends.

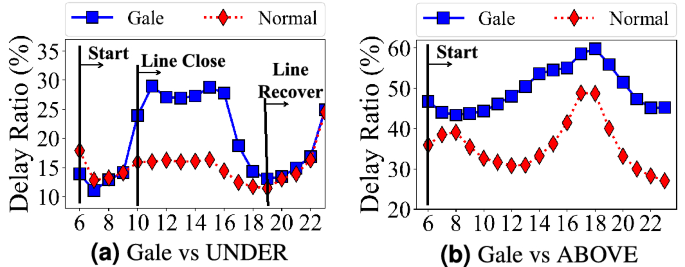
Extreme weather causes high travel delay in both underground and aboveground system; caused (a) subway lines close and (b) low speed on roads.

(4) Weather We group days in 5 years by the level of wind (fresh, gentle, moderate, gale), rain (no rain, light rain, heavy rain), and temperature.

(i) Wind Figure 10a, b show the delay changes in time of day under different wind levels. For the extreme wind weather (e.g, gale), both aboveground system and underground system have higher delay ratios. Through a deeper analysis, we found the delay in the underground system is caused by the temporary closing of some lines and stations where passengers take detours, which leads to higher the underground system delays. But even though some stations and lines may be closed in extreme weather, the underground systems might be more reliable since it can be recovered soon. (ii) Rain For the aboveground system, both the light and heavy rains increase travel delay, especially during peak hours. For the underground system, the light rain increases the travel delay; whereas the heavy rain slightly decreases the travel delay, which is caused by the decrease of passenger demand after analyzing the number of passengers in the subway system. (iii) Temperature Through our analyses, there is no major impact of temperature on travel delay.

(5) Social Events We found different social events have different impacts on travel delay. For example, in the Spring Festival, since most residents leave the city, the travel delay decreases a lot during that time; whereas in the National Day Break, people go shopping and go to local attractions, which leads to a high travel delay.

(6) Crude Oil Prices Figure 11a gives the WTI crucial oil price changes based on the public data records²⁷. The general trend of crucial oil prices decreased from around 100 USD to around 50 USD during year 2012 to years 2018. The correlation analysis is based on the WTI crucial oil price and travel delay ratio change. Since the delay ratio increases in long term due to city expansion and increasing demand, we conduct impact analysis of oil price change in a short-term period. Figure 11b shows the WTI crucial oil price changes on daily basis (relative difference of day two compared with day one). We compared the delay ratio change with the fuel price change in Fig. 11c, in which we found a negative correlation between delay ratio change and fuel price changes. The decrease of fuel price has a higher impact on delay ratio compared with the increase of the price. The potential reason is that the decrease of fuel price will increase the travel demand on above-ground transportation while the increasing price does not impact the travel demand of people who already choose to drive cars to commute. Besides, the impact of fuel price in short term does not impact underground transportation significantly because it does not change the train frequency in the underground transportation system.

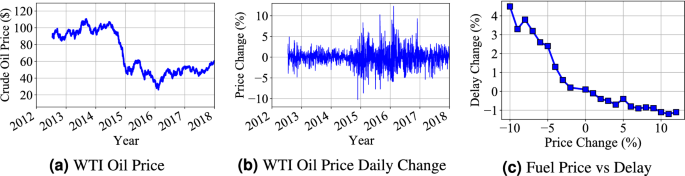
Fuel price change causes the dynamics of delay ratio for above-ground transportation.